面積分割
土地の分割は勿論のこと、
地図を計測したりするのに適宜面積を分割することがあると思います。
面積の分割の仕方は様々ありますが、
ここでは、一般的な方法を見てみたいと思います。
1、面積分割の考え方
面積の分割はどんな複雑な図形でも、
三角形や四角形(四辺形)に細かく分けて計算します。
これは、三角形や四角形の計算なら簡単に出来るからです。
クイズの数学問題で図形が出た時は、
大抵、三角形や四角形に分割して比で計算するやり方になっています。
面積分割も図形を三角形や四角形に分割して比で計算する方法が一般的です。
三角形の面積=底辺の長さ×底辺に対する垂線の頂点までの長さ÷2
正方形・長方形・平行四辺形の面積=底辺の長さ×底辺に対する垂線の上底下底間の長さ
台形の面積=(上底の長さ+下底の長さ)×底辺に対する垂線の上底下底間の長さ÷2
菱形の面積=縦の対角線の長さ×横の対角線の長さ÷2
特に三角形の面積と台形の面積はよく計算に使います。
2、三角形の平行定比分割
三角形は辺の長さと面積には以下の相関関係があります。

三角形の3辺をa倍すると面積はaの2乗倍になります。
例えば3辺それぞれの長さを7倍すれば、面積は49倍になります。
これは、三角形の面積の公式を見ればすぐ分かります。
三角形の面積=底辺の長さ×底辺に対する垂線の頂点までの長さ÷2
三角形をa倍すると、
三角形の面積=a底辺の長さ×a底辺に対する垂線の頂点までの長さ÷2
三角形の面積=aの2乗(底辺の長さ×底辺に対する垂線の頂点までの長さ÷2)
つまり、相似関係の三角形は、
面積の比率=長さの比率の2乗と言う式がなりたちます。
四角形も五角形も六角形・・・も、それぞれこまかく三角形に分けることが出来るので、
他の図形も同じく、上の式が成り立ちます。

先の式から上の図の三角形ABCをm:nに平行分割することを考えてみます。
ぱっと見ると三角形ADEと台形DBCEに分かれるのですが、
三角形と台形だと計算しにくいので、
三角形ABCと三角形ADEに分けて考えます。
三角形ADEは比率m、三角形ABCは比率m+nになるので、
先の式を用いて、
m:m+n=辺ADの2乗:辺ABの2乗
辺ADの2乗×(m+n)=辺ABの2乗×m
辺ADの2乗=辺ABの2乗×m/(m+n)
辺AD=√(辺ABの2乗×m/(m+n))
辺AD=辺AB×√(m/(m+n))になります。
同様に、
m:m+n=辺AEの2乗:辺ACの2乗
辺AEの2乗×(m+n)=辺ACの2乗×m
辺AEの2乗=辺ACの2乗×m/(m+n)
辺AE=√(辺ACの2乗×m/(m+n))
辺AE=辺AC×√(m/(m+n))になります。
3、三角形の1頂点定比分割
一方、1つの頂点を視点として分割する場合は、
もっと単純になります。
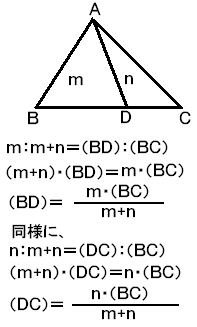
上の三角形ABCを頂点Aからの線で分割する場合、
分けるのは辺BCだけで、あとの辺は分割しないので、
単純な比になります。
m:m+n=辺BD:辺BC
辺BD×(m+n)=辺BC×m
辺BD=辺BC×m/(m+n)になります。
同様の比の考え方で、
辺DC=辺BC×n/(m+n)が求められます。
4、三角形の1定点定比分割
では、一つの辺上の1定点から三角形を分割した場合を考えます。
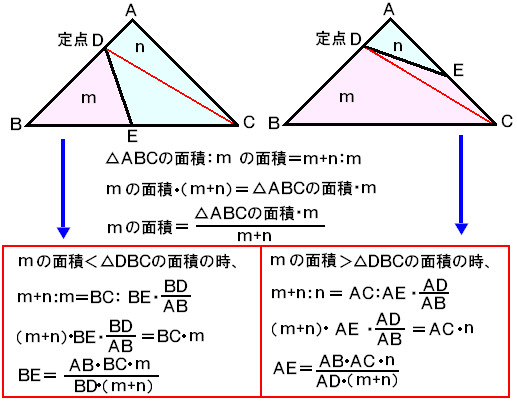
上の三角形ABCをm:nで分ける場合、
点Eの場所が辺BC上になるのか、辺AC上になるのかで、
少し求め方が変わります。
点Eの場所を知るには、
先ず、mの面積と三角形DBCの面積を求めます。
m:m+n=mの面積:三角形ABC面積
mの面積×(m+n)=三角形ABC面積×m
mの面積=三角形ABC面積×m/(m+n)
三角形DBCの面積は辺DB、BCの長さと挟角Bを測り、
辺DB×辺BC/2×sin挟角Bで計算したり、
三辺の長さを測ってヘロンの公式に代入する方法などで計算します。
使い分けは、その辺が視通出来るかどうかで判断します。
ヘロンの公式
S=√(P×(P−辺DB)(P−辺BC)(P−辺CD))
ただし、P=(辺DB+辺BC+辺CD)/2
mの面積が三角形DBCより小さい場合、
m+n:m=辺BC:辺BE×辺BD/辺AB
辺BE×辺BD×(m+n)/辺AB=辺BC×m
辺BE=辺AB×辺BC×m/辺BD×(m+n)
mの面積が三角形DBCより大きい場合、
m+n:n=辺AC:辺AE×辺AD/辺AB
辺AE×辺AD×(m+n)/辺AB=辺AC×n
辺AE=辺AB×辺AC×n/辺AD×(m+n)
5、三角形と台形
台形と言うと「うえっ!?」と思われる方もいるかと思いますが、
台形の左右2辺を延長すると三角形になるので、
台形は三角形の一部分と考えると分かりやすくなります。
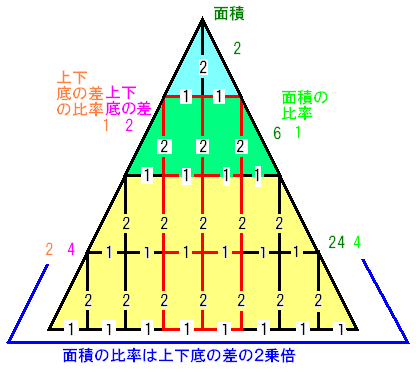
上の図で、緑と黄色の部分はそれぞれ台形ですが、
左右の辺を延長すると頂点のある三角形になります。
台形の面積の比率は、
台形の上底と下底の長さの差の比率の2乗倍と言う相関関係になります。
「上底と下底の長さの差の比率」なのは、
赤線で囲った部分は緑、黄、両図形とも共通の長さだからです。
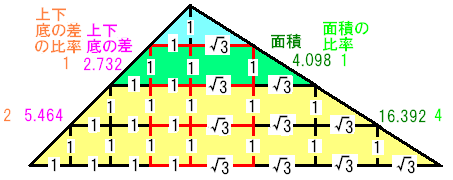
左右の斜辺の角度が異なる場合も面積の比率は、
上底と下底の長さの差の比率の2乗倍になります。
これは、頂点を中心にして2つの直角三角形に分けると分かりやすいと思います。
この法則から台形を平行定比分割する場合の分割線の長さは、
m:n=Lの2乗−上底の2乗:下底の2乗−Lの2乗
m(下底の2乗−Lの2乗)=n(Lの2乗−上底の2乗)
m・下底の2乗−m・Lの2乗=n・Lの2乗−n・上底の2乗
n・Lの2乗+m・Lの2乗=m・下底の2乗+n・上底の2乗
Lの2乗(n+m)=m・下底の2乗+n・上底の2乗
Lの2乗=(m・下底の2乗+n・上底の2乗)/(n+m)
L=√((m・下底の2乗+n・上底の2乗)/(n+m))
例として、上の図の緑+黄色の台形を1:4の面積比率で分ける場合の分割線の長さは、
L=√((1・10.928の2乗+4・2.732の2乗)/(4+1)
L=√(119.421+29.855)/5
L=√29.855
L=5.464
6、台形の1定点定比分割

上の図の台形ABCDを定点Eを基準にm:nに分ける場合、
mの面積と台形ABCEの面積を求めます。
m:m+n=mの面積:台形ABCDの面積
(m+n)・mの面積=m・台形ABCDの面積
mの面積=(m・台形ABCDの面積)/(m+n)
mの面積が台形ABCEより小さい場合、
m:m+n=辺AE+辺BF:辺AD+辺BC
※上の比率の式は、台形mとm+nの面積の公式なのですが、
「底辺に対する垂線の上底下底間の長さ」と「÷2」はmもm+nも同じで、
相殺されるため、省略。
(辺AE+辺BF)・(m+n)=m・(辺AD+辺BC)
(辺AE+辺BF)=m・(辺AD+辺BC)/(m+n)
辺BF=m・(辺AD+辺BC)/(m+n)−辺AE
mの面積が台形ABCEより大きい場合、
n:m+n=辺ED・L2:(辺AD+辺BC)・L1
(m+n)・(辺ED・L2)=(辺AD+辺BC)・L1・n
(辺ED・L2)=((辺AD+辺BC)・L1・n)/(m+n)
L2=((辺AD+辺BC)・L1・n)/((m+n)・辺ED)
境界整正へ
川柳五七の地図のページ6へ戻る
川柳五七の地図のページトップへ
たわたわのぺーじトップへ

|













