地図の面積計測
面積の計測も地図ではよく行なわれます。
面積の計測は多種多様な方法があるのですが、
ここではよく使われる方法をご紹介します。
なお、面積の計測も極力縮尺の大きい地図で行ないます。
※分かりやすくするためにこのページの説明はすべて「水平の土地」と仮定します。
水平の土地でない場合は斜距離で計算します。
1、平面面積計算の基本式
面積を求める場合は先に実際の距離に換算してから計算した方が分かりやすいです。
縮尺が1/Mまたは1:Mの場合
○手順1
地図上の長さを実際の距離にします。
地図上の縦の長さ×M
地図上の横の長さ×M
○手順2
センチメートルやミリメートルの単位をメートルやキロメートルにします。
メートルにする場合概ね「縮尺10000分の1」より大きい縮尺が目安
センチメートルの場合100で割る
ミリメートルの場合1000で割る
キロメートルにする場合概ね「縮尺10000万分の1」より小さい縮尺が目安
センチメートルの場合10万で割る
ミリメートルの場合100万で割る
※注・「縮尺が大きい」とは、1/Mや1:Mの場合、Mの値が小さいことを言います。
○手順3
メートルやキロメートル単位に換算した実際の距離の縦と横の長さを掛けます。
縦の実際の距離×横の実際の距離
メートルに換算した場合は平方メートル、
キロメートルに換算した場合は平方キロメートルの単位になります。
ただ、平方メートルと平方キロメートルはかなり数字の開きがあるため、
(1平方キロメートル=100万平方メートル)
中間の単位としてヘクトアール(ヘクタール)が主に使われます。
1ヘクタール=1万平方メートル=0.01平方キロメートル
2、変形地の計測
計測する土地などが正方形や長方形なら問題ないのですが、
実際は色々な形の土地があり、必ずしも正方形や長方形の土地で無い場合があります。
この場合の計測方法は色々あるのですが、
代表的な5例をご紹介します。
a,方眼法
手持ちに定規と筆記具しかなく、
あまり正確に測る必要性が無い場合は方眼法と言う方法を使います。
これは変形地を方眼に分けて計算する方法です。

上の例図の土地(ここでは湖とします。)を方眼に分けます。
このとき、方眼の1辺は1センチメートル×1センチメートルや、
0.5センチメートル×0.5センチメートルなど計算しやすい正方形で区切ります。
(上の図の例では1センチメートル×1センチメートルで区切ったと仮定します。)
なお、地図に直接筆記具で方眼を区切って汚したくない方は、
トレーシングペーパーか透明のフィルムベースに方眼を書いて計測する部分に当てます。
方眼に分けたら、計測する土地からはみ出ないマスの面積を先に計算します。
1、縮尺が1:Mまたは、1/Mの場合、縦×M、横×M
2、1で出した縦横の実際の距離の単位をメートルやキロメートルに直します。
3、縦×横×マスの個数・・・(1)

計測する土地からはみ出るマスに関しては色々処理方法がありますが、
上の図でははみ出し具合によって1マス、1/2マス、0マスと分けてカウントして計算しています。
(1マスの実際の面積×1マスカウントのマス数)+(1マスの実際の面積×(1/2カウントのマス数÷2))・・・(2)
なお、この他にも1マスを更に細かく4マスに分けてカウントする方法や、
はみ出すマスは長方形にして計算する方法があります。
最後に(1)と(2)を足して面積を出します。
なお、方眼の分け方が荒いとかなりアバウトな面積の数値になります。
b,ドット法
考え方は方眼法と全く同じで、
方眼の代わりにドットの数をカウントして面積を計算する方法です。

トレーシングペーパーや透明のフィルムベースに等間隔で点(ドット)を書きます。
点を書くのが面倒な方は漫画などで使うスクリーントーン(点)をお使いください。
上の図は分かりやすくするために1平方センチメートルにつき1点にしていますが、
実際は1平方ミリメートルくらいにつき1点を配します。
点を書いたらそのトレーシングペーパーなどを計測する土地の部分に被せます。
そして、その土地の中の点の数を数えます。
そうしたら、点の配点間隔の実際の面積に点の数を掛けると答えが出ます。
ドット法の場合、難しい計算はいらないのですが、
点を書いたり、点の数を数えたりするのが面倒なので、
なかなか暇のある方でないと出来ないかもしれません。
c,台形法
これは「積分」を使います。
・・・と、書くと小中学生の方や文系出の方は何が何だか分からないと思います。
平たく言えば細かい台形に分けて計算してそれを合計する方法です。
もちろん、この台形は完全な台形ではありませんが、
台形の分け方を細かくすると限りなく完全な台形に近付きます。
ベーシック言語やC言語などでプログラムが組める方や、
パソコンの表計算ソフト(エクセルなど)を使いこなせる方には便利な方法です。
ただ、一部の世代の方は台形の面積の出し方を習っていないので、
公式を書きますと、
(上底+下底)×高さ÷2
または、(上底+下底)×高さ×1/2
で求められます。
(台形単独では面積の出し方を証明出来ないので、
同じ台形を2つ交互に合わせて平行四辺形として考えて公式を導き出しています。)

方眼法で使った湖で説明しますと、
この池に1センチメートルや0.5センチメートルなどの分かりやすい間隔で平行線を引きます。
(変形地の形によって縦割り横割りを使い分けます。
上の図では1センチメートル間隔にしていますが、実際はもっと細かい間隔にした方が良いです。)
最後端数が出来てしまうので、それは別個に平行線を引き、高さ(幅)を測ります。
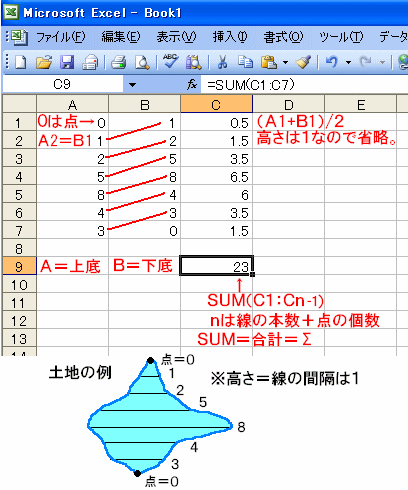
平行線を引いたらそれぞれの台形の面積を求めます。
例えば一番上(北)の台形で言えば、線0=点=0、線1=5センチメートルなので、
(0上底+5下底)×1高さ÷2になります。
次の台形は線1=5センチメートル、線2=6センチメートルなので、
(5上底+6下底)×1高さ÷2になります。
その次の台形もまたその次の台形も・・・同じ要領で計算します。
最後の台形は線6=3.5センチメートル、線7=点=0で、
高さは端数の関係で0.5センチメートルになっているので、
(3.5上底+0下底)×0.5高さ÷2になります。
7つの台形の面積が求められたらそれを合計します。
そして、答えが出たら実際の面積に換算します。
1センチメートル×縮尺M(上の湖の地図はM=25000)÷10万=0.25キロメートル
図上1平方センチメートルの実際の面積=0.25×0.25=0.0625平方キロメートル
図上の面積平方センチメートル×0.0625=実際の面積平方キロメートル
上の図は25000分の1の縮尺地図を1センチメートルで区切ってセンチメートル単位で測っているので、
答えはかなりアバウトになっていますが、
区切りを細かくしたり、縮尺の大きい地図を使うとかなり正確になります。
台形法はいちいち台形の面積を求めなければならないので、
手計算の場合、手間がかかるため不向きです。
しかし、エクセルなどの表計算ソフトを使うと簡単に計算できます。
あらかじめセルに式を埋め込んでおけば数値を入れるだけでいつでも計算できます。
これなら分割間隔を細かく(ミリメートルなど)しても手間がかかりません。
下に簡単な例を載せます。
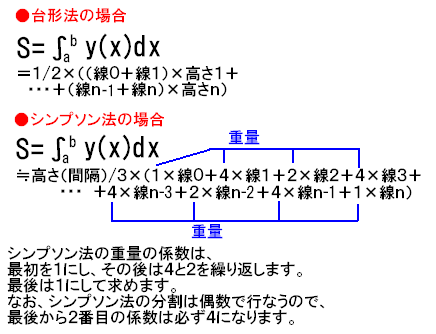
d,シンプソン法
イギリスのシンプソンと言う人が考えた方式です。
考え方は台形法と同じなのですが、
線の長さに重量を掛けることで精度を上げています。
台形法の場合、高さ(幅)は必ずしも等間隔にしなくても良いのですが、
シンプソン法の場合、分割は必ず等分割にして端数を出さないようにします。
しかも分割する個数は必ず偶数にしなければなりません。
分割したらそれぞれの線の長さを測り、
それを足していくのですが、
その前にそれぞれの線の長さに重量と言う係数を掛けます。
係数は最初の線は1にし、その後は4と2を繰り返します。
そうすると最後から2番目の係数は4になります。
最後の線は係数を1にします。
係数を掛けた線の長さの合計が出たら、
それに高さ(幅)/3を掛けます。
あとは実面積に換算するだけです。
シンプソン法は分割数と係数さえ間違えなければ台形法より簡単に計算が出来ます。
e,プラニメーターなどの測定器を使って測る
距離の場合はキルビメーターと言う機械で測れますが、
面積はプラニメーターと言う機械で測る事ができます。
測りたい土地の外周をプラニメーターでなぞると面積が求められます。
キルビメーターと同じくアナログタイプとデジタルタイプがあるのですが、
アナログタイプは少し扱い方法が難しいのと、
手計算が必要なので便利ではありません。
そのため、今はデジタルタイプの方が一般的に使われます。
キルビメーターと同じく購入費用がかかりますが、
頻繁に面積を計測する場合は便利です。
〜おまけ・単位の倍数表〜
よく単位にセンチとかキロとか使われるのですが、
これは基準の単位の倍数を現すものとして使われ、
1キロメートルなら「1メートルの1000倍。」と言う意味で、
1センチメートルなら「1メートルの1/100倍。」と言う意味になります。
ここではその一覧表を挙げておきます。
※数字が大きくなる場合、「10のなんとか乗」と言うのをよく使います。
その時の乗数を出す場合はその数を「log(10底)」にすると出せます。
(関数電卓をお持ちの方は計算してみてください)
なお、「log(10底)」は一般的に「常用対数」と言っています。
表1「倍数表」
| 名称 |
それぞれ1単位あたりの基準単位の倍数 |
| ピコ(p) |
1/1兆(10の−12乗)倍 |
| ナノ(n) |
1/10億(10の−9乗)倍 |
| マイクロ(μ) |
1/100万(10の−6乗)倍 |
| ミリ(m) |
1/1000倍 |
| センチ(c) |
1/100倍 |
| デシ(d) |
1/10倍 |
| 基準単位 |
1倍 |
| デカ(da) |
10倍 |
| ヘクト(h) |
100倍 |
| キロ(k) |
1000倍 |
| メガ(M) |
100万(10の6乗)倍 |
| ギガ(G) |
10億(10の9乗)倍 |
| テラ(T) |
1兆(10の12乗)倍 |
マイクロ(英語)=ミクロン(フランス語)
これらはギリシア語から来ています。
表2「主な単位の換算」
| 1CC=1ml=1立方センチメートル |
| 1ヤード=0.914メートル |
| 1フィート=30.5センチメートル |
| 1ポンド=453.59グラム |
| 1ヘクトアール(ヘクタール)=1万平方メートル |
| 1アール=100平方メートル |
| 1坪=2畳=3.31平方メートル=0.0331アール |
| 1尺=10寸=30.3センチメートル |
| 1里=3.927272キロメートル |
| 1升=1.804リットル |
| 1光年=9460.52テラメートル |
| 1ミリバール=1ヘクトパスカル |
地図の体積計測へ
川柳五七の地図のページ6へ戻る
川柳五七の地図のページトップへ
たわたわのぺーじトップへ

|





