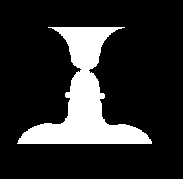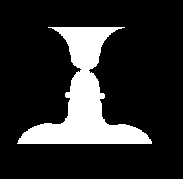地図デザインの基本
地図は「ただ作れば良い」のではなく、
見やすいようにまた、情報を伝えやすいようにしなければなりません。
つまり、「地図をデザインする」と言うことも重要になります。
1、図と地の関係
図と地の関係とは、図形の部分(図)と背景の部分(地)の関係のことです。
地図ではこの図形の部分と背景の部分のバランスが重要だと言えます。
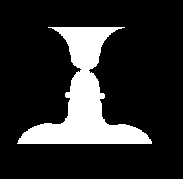
上の絵は「ルビンの壷」と言う絵を弊サイト作者が模写したものです。
白い図の部分だけ見ると普通の白い壷ですが、
黒い地の部分を見ると向き合った人の顔に見える筈です。
(模写した絵が下手で分からないという方はルビンの壷の載っているサイトをご覧下さい。)
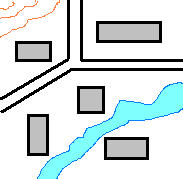
例えばこういう地図の場合、
背景が自然地形(川や等高線)と言うことになり、
図形が家や道路と言うことになります。
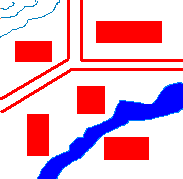
分かりやすく図を赤、地を青にしてみるとなんとなく分かると思います。
この図と地の比率が重要で、
図の比率が高くなりすぎると自然地形が分からなくなり、
読みにくい地図となってしまうのです。
2、データ分級
数値情報(データ)を地図に載せるとき、
そのデータをどのようにまとめて地図に載せるかと言う事が問題になるのですが、
その一手段としてデータの分級と言うのがあります。
データの分級とはデータを等級(クラス)ごとに分けることです。
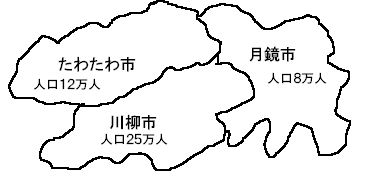
例えば上記3市の人口データを地図に載せる場合、
先ず重要なのはクラスの数とデータ間隔です。

クラスを2つにし、50万人間隔にした場合、
3市とも50万人未満のクラスに入ってしまいます。
これでは地図として何も情報をもたらさないこと(=つまり悪い地図)になります。
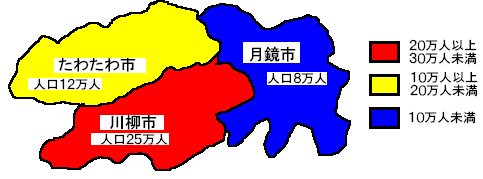
このように適切なクラス分けをすると、
それぞれの情報を読み取ることが出来ます・・・しかしっ!!

分級を細かくしすぎると、情報の区分けが複雑になり、
かえって見難い地図になってしまいます。
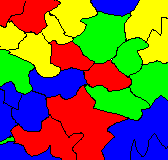
分級は適切に行なうことが必要です。
分級を適切に行なうためには、データの欠落を減らし、
データの精度に見合ったクラス分けをし、
各々のクラス内のデータ数をほぼ均等にさせることが重要です。
おおまかに分類すると以下の表が適切だと言われています。
3、データ分級の種類
データ分級は色々な方法があり、
データの内容や地図の性質等を鑑みて決めます。
a,等分割
クラス内に入るデータ数が同じ数になるように分割します。
b,幾何学分割
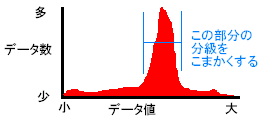
データに偏りがある場合に用います。
データ数が多いところのクラス分けを細かくします。
c,標準偏差分割
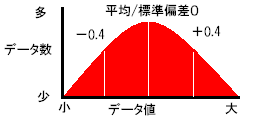
データの平均値を求め、
そこから標準偏差の値ごとに区切ってクラスを決めていく方法です。
上の図のように綺麗な分布になっている場合に最適な方法です。
標準偏差=√((各々の数値−数値の平均)の2乗の合計/データ数)
各々のデータの偏差値=(各々の数値−数値の平均)/標準偏差
受験風偏差値=((各々の数値−数値の平均)×10/標準偏差)+50
d,平均分割
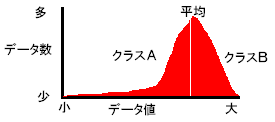
データの平均値を求めて、その平均の値以上と値未満の2クラスに分けます。
更に分けたクラス内の平均を求め、
やはり値以上と値未満の2クラスに分けます(この時点で4クラス出来ます)。
・・・それを繰り返して分割していく方法です。
e,等面積分割
各々のクラスの面積がほぼ等しくするように分割する方法です。
都道府県に分けた場合、北海道のように広い面積もあれば、
香川県のように狭い面積もあるので、
一番広い北海道を基準に等面積分割をすると、
分割数が極端に少なくなる可能性があります。
f,最小2乗法分割
各クラスの平均値を求め、その平均値との各クラス内のデータの差を2乗します。
その値を各々のクラスで合計した後、
全クラスで合計します。
その全クラスの合計数値が最小になれば最適のクラス分けになります。

g,分布曲線分割
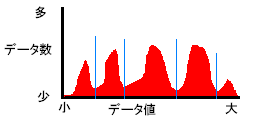
データの山と谷が多くある場合に使う分割方法で、
データの谷ごとにクラスを分けていく方法です。
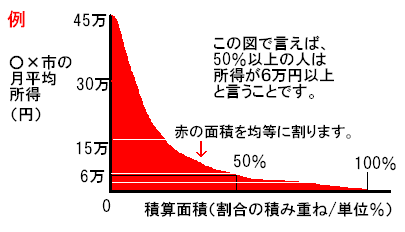
h,積算頻度曲線分割
縦軸にデータ数値、横軸に割合の積算(積み重ね)のグラフを書き、
その曲線面積ごとに割っていく方法です。
i,任意分割
機械的でかつ適当にクラスを分ける方法です。
精度を要する地図には不適当な分割方法です。
4、合計強調
それぞれのデータを強調する場合、
図形を用いて表現します。
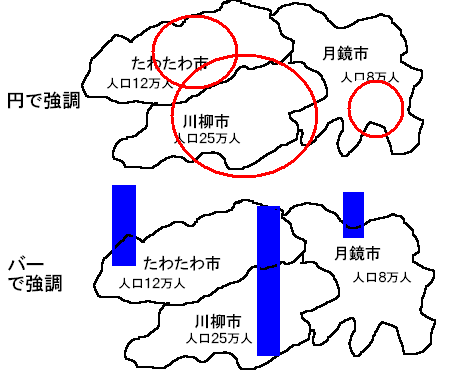
強調に使う図形は円やバーの他、
四角、立方体、級、ブロックの積み重ねなど様々あります。
(学校で使う教材用地図などが参考になります。)
なお、各々の図形を重ねる場合は、
重ねる割合に気をつけます。
(重ね過ぎると分からなくなるし、重ねなさ過ぎるとデータの強調が薄くなります。)
地図表現の種類へ
川柳五七の地図のページ6へ戻る
川柳五七の地図のページトップへ
たわたわのぺーじトップへ

|